By HireHackking in HACKER
· 1 view
des weak necryption easy_blockcipher
添付ファイルをダウンロードして2つのファイルを入手してください：https://adworld.xctf.org.cn/media/task/attachments/5b8b28546b44423b481b13149abc99f.zip 
分析の分析にあります。
des-ofb.py:
crypto.cipher Import desから
f=open（ 'key.txt'、 'r'）
key_hex=f.readline（）[:-1]＃newlineを破棄します
f.close（）
key=key_hex.decode（ 'hex'）
IV='13245678'
a=des.new（key、des.mode_ofb、iv）
f=open（ 'Plantext'、 'r'）
plantext=f.read（）
f.close（）
ciphertext=a.encrypt（plantext）
f=open（ 'ciphertext'、 'w'）
f.write（ciphertext）
F.Close（）は、DESアルゴリズムが暗号化中に使用され、プレーンテキストがOFBモードで暗号化されていることを示しています。
したがって、既知のIV='12345678'の場合、暗号文をクラックするための鍵を知る必要があります。
既知の情報によると、IVと未知のキーのみがあるため、暗号化には弱いキーがあると考えられています。 DES計算では、56bitキーは最終的に16のラウンドキーとして処理され、各ラウンドキーは16ラウンドの計算に使用されます。 DES弱いキーは、これらの16の丸いキーが完全に一貫しているため、弱いキーと呼ばれます。
弱いキーの4つは次のとおりです。
0x000000000000000
0xffffffffffffffffffffffffff
0xe1e1e1e1f0f0f0f0
0x1E1E1E1E0F0F0F0Fは、4セットのキーを使用して、暗号文をクラックしようとします。
crypto.cipher Import desから
f=open（ 'ciphertext'、 'r'）
ciphertext=f.read（）
f.close（）
IV='13245678'
key=b '\ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00 \ x00'
a=des.new（key、des.mode_ofb、iv）
plantext=a.decrypt（ciphertext）
プレーンテキストを印刷します
key=b '\ x1e \ x1e \ x1e \ x1e \ x0f \ x0f \ x0f \ x0f \ x0f'
a=des.new（key、des.mode_ofb、iv）
plantext=a.decrypt（ciphertext）
プレーンテキストを印刷します
key='\ xe1 \ xe1 \ xe1 \ xe1 \ xf0 \ xf0 \ xf0 \ xf0 \ xf0'
a=des.new（key、des.mode_ofb、iv）
plantext=a.decrypt（ciphertext）
プレーンテキストを印刷します
key='\ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff \ xff'
a=des.new（key、des.mode_ofb、iv）
plantext=a.decrypt（ciphertext）
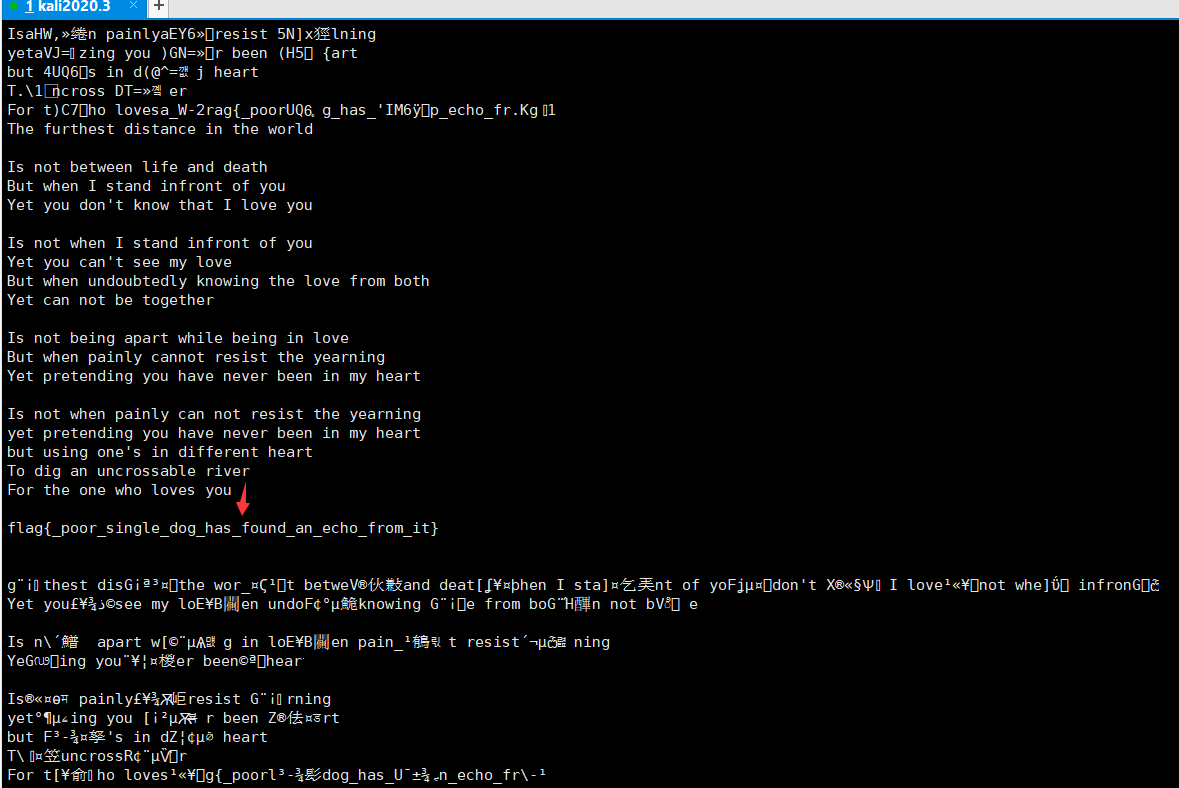
得られた結果からの印刷のプレーンテキストは、シェークスピアによる詩です。
またはスクリプト：＃Coding:UTF-8
crypto.cipher Import desから
libnumをインポートします
ct=open（ 'ciphertext'、 'rb'）。read（）
key=libnum.n2s（0xe0e0e0e0f1f1f1f1）
IV='13245678'
a=des.new（key、des.mode_ofb、iv）
印刷a.decrypt（ct）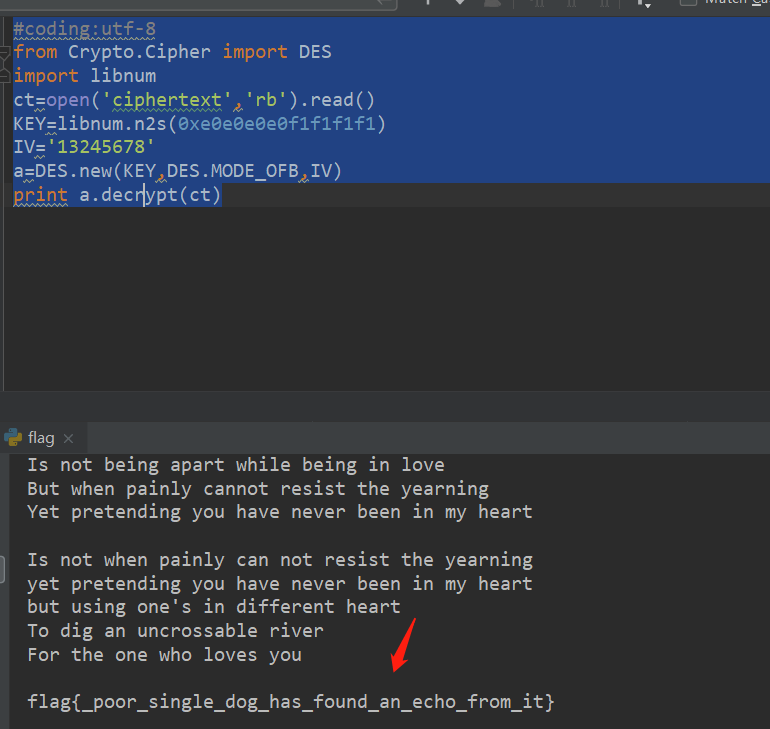
が最後にflag:flag {_poor_single_dog_has_found_an_echo_from_it} :010101010質問説明：RSAアルゴリズムを学習するとき、私は同じセキュリティと同じセキュリティと同じセキュリティを持っていることを発見しました。 MSG.TXTを暗号化しますMSG.ENCを取得します。 $ python special_rsa.py enc msg.txt msg.enc flag.encからflag.txtを回復できますか？次のように、4つのファイルを含む添付ファイルをダウンロードしてください：https://adworld.xctf.org.cn/media/task/attachments/7a407f44a073442c91fd395b20594f01.zipflag.encenc
Special_rsa.py
msg.enc
msg.txt
質問のアイデアは、隠されたキーを使用してflag.encファイルを復号化することです。 Special_rsa.pyファイルの暗号化と復号化プロセスを読んだ後、隠されたキーを見つけるための簡単な式を作成しました。
擬似コードは次のとおりです。
flag.sage:
n=239274110140220695772934916764953661641310148480977056645255098192491740356525 24067590628570051635757892994011455370097616796996436414961522656868688922422802 846168661729353411578877799955597877965045704934575674208747413571865964257536 67455266870402154552439899664444136327167476448548975519407777512522049071328 64905644212655387223302410896871080751768224091760934209917984213585513510597 619708797688705876805464880105797829380326559399723048092175492203894444875271 8008631464599810632513162129223564676025080953565844055553290961599179573898 34381018137378015593755767450675441331998683799788355179363368220404088888888888888888888871713131L
C1=1454899738089726523978888482538130110996551898966180809068895223232381091726761 46495957294338302442802827071762995389459289085912881883932849900295082849152 1254480795364789013196240119403187073307558598496713832435709741997056118318 6037022715563316901966556439264952830698682696082941012034891358659219732730 93325988046922972414988738000562732175284348956498435870801330052464054543770 377142416810821304556756859509342136622481860950131878368049776353536181101840 78118456368631056495264337304089769880146783912055298782061128568056163894 01039724530142567623212626787465671025683845772894370612289985071385621160886
C2=12793942795110038319724531875568693507469327176085954164034728727511164833535 10175515351403025615287836466407905656538533190119654101539360975162497155401 66711607304789323439495382021675083192920845196217688518785266570229818833042 6088684151342396524869530063372782511380879783246034751883691295368172069170 96797556136427514063320691930900258017293871754252220972730171920769232179822222 9276732198521711602080244950295888957542338330809978629818447766830282842952156 657346718292493236040323206962671303306131343686404010707759271975554082071807 605399448960911234829590548855031180158567578928333030631307816223152118126597
M1=82460741826420911255783118283748436989942332438113476912293348292187007286240 47916518503687366661595620990394114306629686684708665972123162319899501758 42479609181025988465333257613612814495875132784474699126466700735951818136352 2934430676655236880489550093852524801304612322373542296281962196795304497110 06801211783005857297362930338978872451934860435597545642219213551685973208209 8736239096292783211814850109644606529869005874709029831236523067172379085099 85419566643768208205707092725003309662055788986903967066950240019707278640914 3651820241416691902041589276461705597848899616464222958271749337541999999360
M2=155750514538585217531084620637237509863860930677639483166121579461908355552732641412018370629510122222222222227815564183091664 7308058835456242606669492436488691640815057608266779727400066172627987197137743836282940252968282547129986181482946 351065925858602073222835125829152796582297704895472055897384095673137732251616880937364049422712999887116708958968 979602445850170570477910915276237366054268488800524892130399992038375799308553003385290580003301033333333333333333396323251274293258
R1=12900676191620430360427117641859547516838813596331616166760756921115466932766 990479475373384324634210232168544745678883988849094363202992624666063289599443
R2=7718975159402389617924543100113967512280131630282866240781023681661854434662628 61344357647019797762407935675150925255550347533663981198198412652955767981059
_、a、b=xgcd（r1、r2）
k=pow（（c1/m1％n）、a、n） * pow（（c2/m2％n）、b、n）
印刷（k）
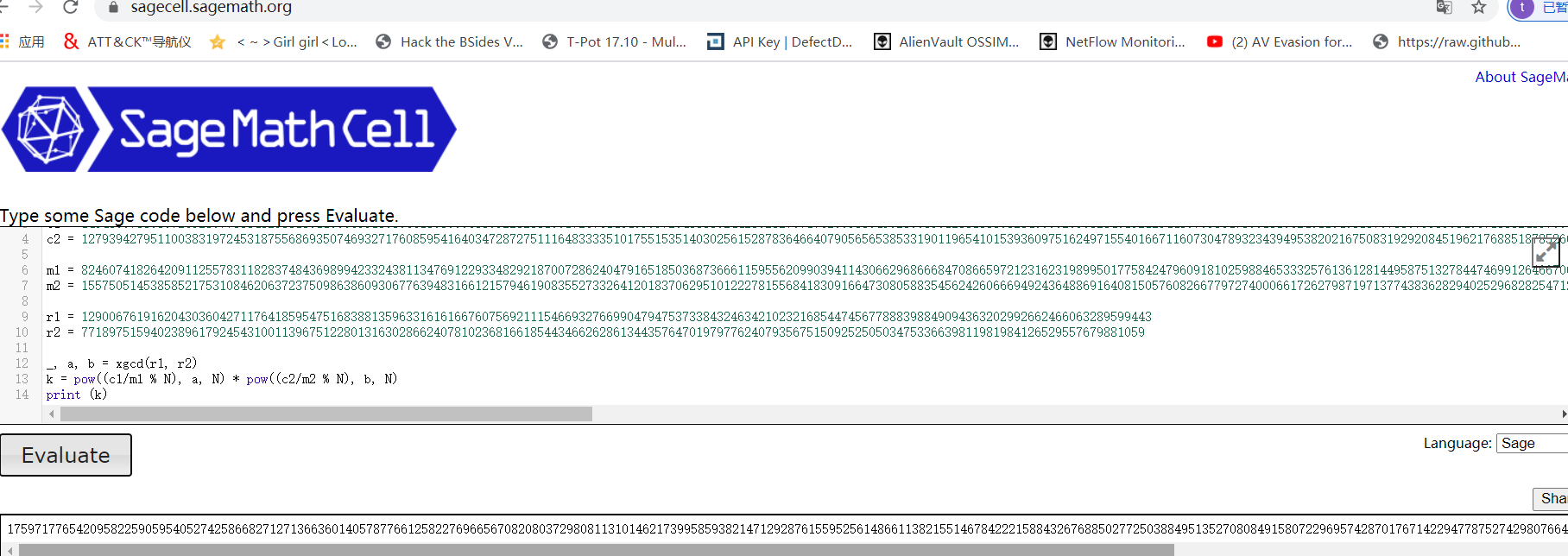キーを取得：
175971776542095822590595405274258682712713663601405787766125822769656708208 0372980811310146217399585938214712928761559525614866113821551467842221584326 7688502772503884951352708084915807296957428701767142294778752742980766436072 18336744447622123999867771240935016192735134218031773471810632544214926211961
キーを取得し、flag.encをDecrypt、答えを取得します：
ポートmsgpackdef egcd（a、b）: a==0: return（b、0、1）else: g、y、x=egcd（b％a、a）return（g、x-（b //a） * y、y）def modinv（a、m）: g、x、y=eg=eg=eg g pad_even（x）: return（ ''、 '0'）[len（x）％2] + xdef decrypt（c、k）: out='' r_s、c_s in msgpack.unpackb（c）: r=int（r_s.encode（ 'hex'）、16）c=int（c_s.c_ modinv（k、n）out +=pad_even（format（pow（k_inv、r、n） * c％n、 'x'））。デコード（ 'hex'）return outn=239274110140220695772934916764953661641310148480977056645255098192491740356525 24067590628570051635757892994011455370097616796996436414961522656868688922422802 846168661729353411578877799955597877965045704934575674208747413571865964257536 67455266870402154552439899664444136327167476448548975519407777512522049071328 64905644212655387223302410896871080751768224091760934209917984213585513510597 619708797688705876805464880105797829380326559399723048092175492203894444875271 8008631464599810632513162129223564676025080953565844055553290961599179573898 34381018137378015593755767450675441331998683799788355179363368220404088888888888888879117131K=17597177654209582259059540527425868271271366360140578776612582276966567082080 37298081131014621739958593821471292876155952561486611382155146784222215884326768 85027725038849513527080849158072296957428701767142294787527429807664360721833 6744476221239999867771240935016192735134218031773471810632544214926211961PRINT decrypt（open（ 'flag.enc'）。read（）、k）
最後にflag3360を取得しました
flag: bctf {q00000000000b3333333333 -ju57 -w0n -pwn20wn !!!!!!!!!!
タイトルは、flag.encとpublic.pemを与え、添付ファイルのダウンロードアドレス：
https://adworld.xctf.org.cn/media/task/attachments/9244cc370caa43f491636f8c4670fe7d.zip
OpenSSLのインストールは、nとeを読み取ることができます。 nは大きくないため、yafuまたはfactordb.comで分解してn=p * q * rを取得できます
flag.encによれば、暗号文mを取得できます
中国の残留定理によると、P、Q、R、およびPMOD、QMOD、RMOD、RMODに設定される可能性があります。
次に、残りのモードに3回、つまり、prot ^ 3 pmod（mod p）、find：prot、同じことがqroot、rrootにも当てはまります
Webツールを使用すると、直接計算できます。
http://www.wolframalpha.com/input/?i=x%5E3+%3D+19342563376936634263836075415482+(MOD+27038194053540066199904565656526063）
RSAを介して暗号化されていると思われるOpenSSLコマンドラインから暗号文を取得します。また、公開キーにもアクセスできるため、標準のRSAパスワードを使用するのと同じように、パラメーターを復元することで以下を実行します。
E=3
n=232927109786703804036412732700028847470600065680462900119184133754739340240397151805408873380677
Yafuを使用して、モジュラスを以下に分割します。
P=264406153663952421965168534447
Q=27038194053540661979045656526063
R=3258147930040487672405716877547
3つの素数が得られます。これはまだ良いことであり、単に多品質のRSAかもしれません。これはまったく驚くことではありません。一般的に言えば、それは非常に単純（P-1）（Q-1）（R-1）であり、残りの計算は通常どおりに実行されます。しかし、モジュラー乗算の逆が存在しないことがわかったため、それは存在しません。理由は明らかです。GCD（e、クライアントへ）=3、1である必要があります。これは、同様の状況に遭遇したのはこれが初めてではありません（https://github.com/p4-team/ctf/tree/master/2015-10-18-hitcon/crypto 314-u rsabin-35; engバージョン）。
RSAデコードを適用する前に、これら3を削除する必要があります。これは、暗号化が次のことを意味します。
ciphertext=plaintext^e mod n=（plantext^e '）^3 mod n
したがって、方程式の両側に弾性キューブルート（mod n）を形成できる場合、RSAデコードにE '=e/3を使用できます。 e=3、e '=e/3=1なので、ここでは簡単ではありません。つまり、暗号化は簡単です。
ciphertext=plaintext^3 mod n
したがって、復号化プロセス全体には、暗号文のmodキューブルート（mod n）が必要です。
カビの根についてのいくつかの読みは、これが可能であるが限られた領域でのみ結論に至ることにつながります。したがって、それはnではできません、それは複合数であり、それがPQRだからです。
この質問は、中国のリマインダー定理（https://en.wikipedia.org/wiki/chinese_remainder_theorem）を思い出させます。しばらく考えた後、Ciphertext（mod Prime）から3つのプライムの3回のカビの根を計算できれば、マージの根を計算できるという考えを思いつきました。 Gaussian Algorithm（http://www.di-mgt.com.au/crt.html#gaussalg）を使用してこれを達成できます。
したがって、私たちは計算を続けます：
pt^3 mod p=ciperhtext mod p=2082790798810303030784078915883129
pt^3 mod q=ciperhtext mod q=19342563376936634263836075415482
pt^3 mod r=ciperhtext mod r=1052528394780776022788040671000
その後、このPTの方程式を解くのにしばらく時間がかかりましたが、最後に、Wolframalphaがこの機能を実装することがわかりました。
http://www.wolframalpha.com/input/?i=x^3+％3d+2
Recommended Comments